Talk:Lattice (order)

Atomistic property

There is a mistake in the characterization of atomistic property, as now, it contradicts transitivity of the lattice order. — Preceding unsigned comment added by 210.74.131.204 (talk) 09:13, 9 July 2018 (UTC)[reply]

Map of lattices

For the moment, I have added a "See also" link to my Map of lattices. It may be useful to have it figure more prominently in this article in the future.

I have transferred the discussion on the content of the map (as opposed to how to use it) to its talk page.

Non-negative integers

The list of examples of complete lattices contains this item:

The non-negative integers, ordered by divisibility. The supremum is given by the least common multiple and the infimum by the greatest common divisor.

What is the least common multiple of an infinite set of non-negative integers? How is this lattice then complete? It's not even bounded, is it? Am I missing something? Also, the issue of completeness aside, should that be positive integers?

Or have I just answered my own question? Zero could be considered the least common multiple of an infinite set, and a bound on the lattice. But then least here doesn't refer to the usual ordering of the integers, or zero, if considered a multiple of everything, would be the least common multiple of every set. Perhaps a little more explanation is in order Josh Cherry 23:26, 8 Jul 2004 (UTC)

Yes, that is basically correct: "least" and "greatest" refer to the given order of divisibility, not to the normal total order of integers. 0 is then the greatest element: it is divided by any number. 1 is least: it divides any number. Infinite sets have only 0 as an upper bound, while they may have numbers other than 1 as a lower bound (like 2 in the case of all even numbers). I will add some remarks... --Markus Krötzsch 14:57, 15 Jul 2004 (UTC)

Cool, thanks. I added a sentence to that section. Please verify that it's correct. Josh Cherry 22:15, 15 Jul 2004 (UTC)

Yep, that's true. --Markus Krötzsch 14:03, 20 Jul 2004 (UTC)

Examples?

I've moved the following "Examples" section to here for reasons stated below:

* For any set A, the collection of all finite subsets of A (including the empty set) can be ordered via subset inclusion to obtain a lattice.

* The natural numbers in their common order are a lattice.

* None of the above lattices is bounded. However, any complete lattice especially is a bounded lattice.

* The set of compact elements of an arithmetic (complete) lattice is a lattice with a least element.

Reasons for move:

The statement "None (neither?) of the above lattices is bounded." is not correct for the first example if A is finite. (I presume that the first example was meant to have A infinite?)
I don't understand the fourth example, what is an arithmetic (complete) lattice, is this defined somewhere? Why is complete in parenthesis? Is it meant to define arithmetic?
The placement of this section seems out of place to me. I think the examples of unbounded lattices should be closer to where bounded is mentioned. Same goes for the observation that every complete lattice is necessarily bounded.
Although I think this content should be included in the article, since I couldn't quite make out how to fix it, I've moved it here for someone else to have a look at. ;-)

Paul August 18:16, Sep 3, 2004 (UTC)

Agreed, some things here needed reconsideration. I put the list back into the article after the following fixes (refering to your comments):

True.
True: the article on arithmetic lattices needs to be written. It is a concept from domain theory, basically an algebraic lattice (i.e. a Scott domain that is a complete lattice) where the compact elements form a lattice. "Algebraic" and "arithmetic" is usually assumed to imply "complete" when applied to a lattice. Since this is not always the case, I added the term in parentheses.
Yes, I moved it upwards. The downside i, that some properties are only defined afterwards, but eventually all of these special lattices should have their own articles (including examples) anyway.
Well, a reasonable choice. However, I feel that there should be some prominent "examples" section in such an article (in the worst case just with a remark), in order to give newcomers a place to add some nice examples (Possible course of events: someone finds a reference to lattices without knowing the details, looks up the net, finds Wikipedia, and may want to contribute the example that caused her search in the first place -- I'm always optimistic ;-).

--Markus Krötzsch 20:45, 14 Oct 2004 (UTC)

Much better ;-). Paul August 21:13, Oct 14, 2004 (UTC)

Top and bottom

I'm surprised this article doesn't talk about top and bottom anywhere, although it does use the terms (with no defining link). Are these described elsewhere or this something that should be added? Deco 18:52, 16 December 2005 (UTC)[reply]

Those are not technical terms. I guess someone used those terms to try to be friendlier to laymen. The definition of bounded lattice can be found later down the article: a bounded lattice is a lattice with a least and greatest element. The words "top" and "bottom" are more or less meaningless. Maybe they make sense when you have the Hasse diagram of the lattice in front of you, vertically aligned. -lethe ^talk 19:12, 16 December 2005 (UTC)

Well, I've encounter them a lot in classes and such. They seem to be conventional names for the least and greatest element of a bounded lattice, in the same way that p is a conventional name for a positive prime integer. I think they're frequently used enough to justify mentioning, at least in passing. Deco 20:37, 16 December 2005 (UTC)[reply]

I've never heard that before in my life, though surely there are a lot of things I've never heard of. But can you tell me a textbook that uses that terminology, if you know one off-hand? I'd like to see it for myself. -lethe ^talk 21:08, 16 December 2005 (UTC)

Davey and Priestley, Introduction to Lattices and Order (ISBN 0521784514) uses top and bottom. As far as I now they are in fact technical terms, at least in domain theory and its applications to denotational semantics. — Tobias Bergemann 22:48, 16 December 2005 (UTC)[reply]

Also see greatest element. — Tobias Bergemann 22:58, 16 December 2005 (UTC)[reply]

Ah, that's why they're familiar to me. I encountered them in programming language semantics. I also encountered them studying compiler optimizations like sparse conditional constant propagation. Seems CS people like them. Deco 23:29, 16 December 2005 (UTC)[reply]

My readings so far in quantum physics and statistical mechanics and set theory and such has led me to seriously wonder whether how much of quantum physics actually knows of mathematics. When I saw top and bottom I jumped right in to find out whether, as one would maybe expect, the quark model people knew full well what top and bottom were when they labelled the top quark and the bottom quark.

If it is true that top and bottom as in quarks does not relate to top and bottom as in lattices why do I have haunting vague hand-waving recollections of having recently read a lot of quantum physics that hand-waved in the direction of lattice and/or gauge theories? (Note: I am on lattice right now, have to get to guage soon, so dunno if gauge even had anything to do with lattice.

Basically what is bothering me is a haunting suspicion that cardinality and catastrophe and 'phase transitions' and such, that call for mysterious new 'bosons' mediated by coloured mediators and such, and mysteriously conjure mass into and out of existence, might be related. Markovianism is in the brew too: if each cardinality pretty much amounts to a markovian 'past events horizon' up to which all previous history is pretty much 'moot', a lattice might be precisely what the quark people are squeezing in between the bottom catastrophe (the cardinality below) and the top catastrophe (the cardinality above) of the tiny space in which they are waving their hands and invoking 'Quantum Mechanics' (maybe in one cardinality regime?) and 'Quantum Chromodynamics' (maybe in another cardinality regime) about?

Maybe I am just seeing too many coincidences? But cardinality also seems to potentially be referrable to orders of logic, and certainly the logic of quantum physics expositions that I have been reading does seem to involve different orders of logic. Cardinality might not be the right word, I am trying to refer to aleph null and upwards, the infinities that are whole orders above each other. Are quantum folk making lattices that bottom out at one of those infinity levels and top out at the next, something like that? Thus using the terms top and bottom from lattice theory?

If top and bottom do truly have nothing to do with quarks do please elucidate that fact.

Knotwork 05:25, 24 August 2006 (UTC)[reply]

I think it's even worse. As far as I know (I could be wrong, though), the lattice theories in physics have nothing at all to do with lattice (order), but are somehow related to lattice (group). Which is something entirely different. --Hans Adler (talk) 10:52, 18 April 2008 (UTC)[reply]

Idempotent laws as a consequence ?

This article states that the idempotent laws follow from the associative, commutative and absorption laws of a lattice. I think they don't. If anyone can construct a brief proof, please send it, otherwise the article should be corrected. Nidus 14:21, 17 February 2006 (UTC)[reply]

Nidus is quite right. The idempotent law is not a consequence of the others. Consider the counter example where $a\wedge b$ is the union of $a,b$ plus a single element $x$ and $a\vee b$ is the interesection of $a,b$ minus a single element $x$ . Verify that the associative, commutative and absorption laws hold but the idempotent doesn't. The article should be corrected! —The preceding unsigned comment was added by 130.130.37.6 (talk • contribs) 00:50, 23 March 2006 (UTC1)

A short proof of the idempotent laws: The first absorption law gives us $a=a\wedge (a\vee b)$ . Replacing $b$ with $a\wedge c$ we get $a=a\wedge (a\vee (a\wedge c))$ . Since $a\vee (a\wedge c)=a$ by the second absorption law we get $a=a\wedge a$ . The proof of the other idempotent law is dual to this one.

The absorption laws do not hold for the operation given in your counter example:

S\wedge (S\vee T)=S\wedge (S\cup T\cup \{x\})=(S\cap (S\cup T\cup \{x\})-\{x\}=S-\{x\}

So the absorption law does not hold if $x\in S$ . —Tobias Bergemann 13:40, 23 March 2006 (UTC)[reply]

I miss the argument why

b

can always be written as

a\wedge c

.

In general there is no such and thus the article should be corrected.

Actually if we require distributivity the idempotent law can be prooven:

a=a\vee (a\wedge a)=(a\vee a)\wedge (a\vee a)

a=a\wedge (a\vee a)=(a\wedge a)\vee (a\wedge a)=(a\vee (a\wedge a))\wedge (a\vee (a\wedge a))=((a\vee a))\wedge (a\vee a))\wedge ((a\vee a)\wedge (a\vee a))=a\wedge a

—The preceding unsigned comment was added by 85.124.7.101 (talk)

You wrote: "I miss the argument why $b$ can always be written as $a\wedge c$ ." You don't need this, all you need is that

a=a\wedge (a\vee (a\wedge c))

for every

a

and

c

, and this is true because

a=a\wedge (a\vee b)

holds for every

a

and

b

and therefore specifically holds if

b=a\wedge c

. —Tobias Bergemann 07:34, 2 May 2007 (UTC)[reply]

Dual lattices

If no one objects within a couple of days, I'll add a section on dual lattices (reversing the partial order, or, equivalently, substituting meet by join and vice versa). This duality is pretty obvious to any lattice theoretician, of course, but not necessarily so for the readers. It is interesting in itself, and I'd like to refer to it in order to clarify why e.g. meet-semilattices and join-semilattices coincide as abstract algebraic structures. I also found no other article dealing with this particular duality.

(Actually, it might be possible to outline connections to other kinds of duality. E.g., recall that if $(L,+,\cap )$ is the (modular) lattice of all subspaces of a finite-dimensional vector space V over a field k, then the dual lattice may be canonically identified with the lattice of subspaces to the dual vector space $V^{*}=$ Hom $(V,k)$ , by letting W ∈L correspond to $\{f\in V^{*}:f(W)=0\}$ . However, I suspect that this would lead too far for the Lattice (order) article.) JoergenB 18:42, 21 September 2006 (UTC)[reply]

Applications?

Quoting: "Distributivity is too strong a condition for certain applications" Such as??? What is ment by applications? -kaz

It is not lattice on picture

Partially ordered set, shown on picture, is not a lattice! For example, elements 1234 and 12/2/4 have no infimum. Dims 05:20, 16 January 2007 (UTC)[reply]

Are you sure? If you mean 1234 and 12/3/4 then their infimum is 12/3/4 and their supremum is 1234 as 1234 > 12/3/4. --- Richard CHS^Talk 22:49, 18 January 2007 (UTC)[reply]

Acyclic?

Is a lattice necessarily acyclic? If so, that is a key fact that would be helpful to mention explicitly. Based on reading the definitions of supremum and infimum, I would assume that a lattice is acyclic, but not being well versed in this area of mathematics I would have to spend much more time reading and thinking it through to convince myself with certainty, so it would be nice to simply hear it from an expert. Of course, implicit here is the fact that I'm thinking of a lattice as a kind of graph, which I hope is a reasonable way to think about it, and one which I also think would be helpful to mention. Thanks. -- DBooth 21:40, 22 January 2007 (UTC)[reply]

It's easiest to see that they're acyclic by the requirement of partial-orders that a≤b and b≤a imply a=b. Combined with transitivity of the ordering relation, this means that a cycle of two or more distinct elements is impossible. -- Sswords 05:24, 26 January 2007 (UTC)[reply]

Morphisms

The article defines morphisms like this:

Given two lattices (L, $\vee$ , $\wedge$ ) and (M, $\cup$ , $\cap$ ), a homomorphism of lattices is a function f : L → M such that

f(x $\vee$ y) = f(x) $\cup$ f(y), and

f(x $\wedge$ y) = f(x) $\cap$ f(y).

Thus f is a homomorphism of the two underlying semilattices. If the lattices are bounded, then f should preserve the bounds so that:

f(0) = 0, and

f(1) = 1.

Is preservation of bounds part of the definition of morphism, or is it supposed to follow from the other two requirements? Wouldn't, say, f : {0,1} → {0,1} with f(x) = 1 be a counterexample?

Sswords 18:54, 25 January 2007 (UTC)[reply]

The preservation of bounds does not follow from the preservation of ordinary (i.e., binary) join and meet, as your counterexample shows. Actually, the more structure you add to your concept, the fewer of the functions will respect all of them. Thus, properly you should distinguish between "morphisms in the category of lattices", "morphisms in the category of bounded lattices", and "morphisms in the category of complete lattices", where you have joins and meets defined only for non-empty finite families of lattice elements, for all finite families, or for all families of any cardinality, respectively. (Technically, in this case the category with more structure is a subcategory of the one with less structure, but not an full subcategory. However, that is just a fancy way to sum up what we already said.)

You may also consider the lattice categories as non-full subcategories of the category of posets. Indeed, demanding only that meet be preserved, or only join, or only the partial order, yields different sets of morphisms between the same two lattices. I do not think that all this should be explained in the article, though. JoergenB 08:29, 25 February 2007 (UTC)[reply]

The primary examples of what JoergenB is talking about are frames and locales, which are cats both having the same object, but having different morphisms. linas 14:20, 8 June 2007 (UTC)[reply]

Free lattice

I'm thinking of moving the section called "free lattice" to its own article; would there be objections to that? linas 16:40, 6 April 2007 (UTC)[reply]

I'm gonna do it, unless someone says no...linas 04:34, 19 April 2007 (UTC)[reply]

Done. See Free lattice. linas 14:18, 8 June 2007 (UTC)[reply]

Conditions for a poset to be a Lattice

I'm not a mathematician at all, but I'm dealing with a physical model that can be viewed as a poset - yet I'm not certain at all if it is a lattice.
The graph structures produced are always most disordered and complex, and it's not easy to grasp if inf{} and sup{} do exist always.
I was wondering if some rule of thumb exists, to judge the lattic-ity of a poset.
E.g. if a poset is 1) connected and 2) does not exhibit a "butterfly" pattern (fig.2.1(ii) in "Introduction to Lattices and Order") is it a lattice?

references:
G. Bertotti, P. Bortolotti, A. Magni, V. Basso Topological and energetic aspects of the random-field Ising model J.App.Phys.101(2007)09D508
P.Bortolotti, A.Magni, V.Basso, G.Bertotti Dynamical-system theory approach to the study of metastable states in the random field Ising model J.Magn.Magn.Mat. 310(2007)1543-1545

thanks for any hint, 193.204.114.65 10:07, 7 August 2007 (UTC) Alessandro Magni[reply]

Examples of posets which are not lattices

I want examples of (infinite) partially ordered sets which are not lattices and even not semilattices.

porton (talk) 18:10, 28 November 2007 (UTC)[reply]

The purpose of this page is to discuss improvements to the article. This question belongs on Wikipedia:Reference desk/Mathematics instead. Michael Slone (talk) 20:26, 28 November 2007 (UTC)[reply]

But giving examples of posets that aren't lattices is an improvement to the article. I gave a few such counterexamples just now, all finite but they're easily made infinite by disjointly adding any infinite poset. --Vaughan Pratt (talk) 21:29, 2 December 2009 (UTC)[reply]

Or there is an other type of lattice.This lattice is where your are doing mutiplication. You are going to set up the problem like a window and then after that you will cut each little square. After that you will put the number(s) on top of the square and then the other number(s) will go on the side and you will start the problem.when you are doing multiplication you will times the numbers and add all of them together and you will get you'r factor. —Preceding unsigned comment added by 69.239.138.181 (talk) 01:22, 14 February 2008 (UTC)[reply]

That's Lattice multiplication and it has very little to do with the theory of partially ordered sets. —David Eppstein (talk) 01:25, 14 February 2008 (UTC)[reply]

Partially ordered set or poset

"In mathematics, a lattice is a partially ordered set (or poset)": Ambiguous? I am guessing that it means "In mathematics, a lattice is a partially ordered set (a poset)" but I have not the expert knowledge of the topic necessary to be certain that is in fact what it means, rather than what it well might, taken as English, mean, to wit that it is EITHER a partially ordered set (see explanatory link if not sure what that means) OR a poset (oops no clickability of this term so no idea what the heck does it mean).

My immediate impulse as a Wikipedia Proofreader was to edit it to change 'or' to 'a' in order to make it less susceptible to being interpreted the wrong way, aka IMO to make it 'less ambiguous' aka 'more clear'. But what if the author already did this soul-searching, determined with mathematical rigour that 'a' would be incorrect, that 'or' is correct, yet somehow managed to neglect to make 'poset' an active hyperlink? I guess the reader should first search for themselves to discover whether there is or is not an entry in the Wikipedia explaining what a poset is? Maybe I should do that search and if such a page exists make 'poset' an active link?

I dunno, would using 'a' instead of 'or' be such an awful thing that all this extra work is preferable to using the term 'a' instead of the term 'or' ???

Knotwork (talk) 09:20, 18 April 2008 (UTC)[reply]

Fixed. I have also moved your comment down and added a title. It's better to use the little "+" at the top of the talk page to start a new topic. --Hans Adler (talk) 10:46, 18 April 2008 (UTC)[reply]

Fonts needed by Wikipedia

Hi - my computer won't display the meet and join symbols in the article. What do I need to do? Thanks

I enlarged the first image to make it readable.

Nice article.SteveWoolf (talk) 21:20, 22 November 2008 (UTC)[reply]

What you need to do depends on your operating system and on your browser. E.g. I have never had such problems with Firefox on my EeePC. Under Windows XP I have a somewhat unusual setup in that I installed lots of free fonts from a CD, which may make a difference. Firefox also displays everything correctly there, but for some reason Internet Explorer doesn't. However, on my computer Internet explorer has no problems with the small lattice symbols (only with one of the two big ones).

There is some technical help here. Please let us know if that helps in your case. If not, and if you are using Internet Explorer, you should really consider trying Firefox instead, since this seems to be a common problem with Internet Explorer. --Hans Adler (talk) 01:01, 23 November 2008 (UTC)[reply]

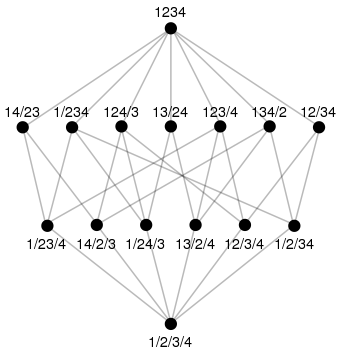
Which Hasse diagram?

I have included a new Hasse diagram with an external legend, and they have been replaced by the old diagram - possibly because of the second graphic. I created a new version with the description in the diagram, as it is in the old one. Unlike Hans Adler I think the new diagram is better. Which one is easier memorized and drawn freely on a blackboard? And which one tells more about this lattice? In the old graph it's not easily seen, that the elements 0,...,4 form a subgraph, and thus a sublattice - and it's not easily seen, that the elements 8,9,10 are different in their nature from the elements 4,11,12,13. The knots may look more tidily arranged in the old diagram, but without respect for the edges between them. So I see no reason, why the old diagram should be preferred.

Lipedia (talk) 16:53, 15 March 2010 (UTC)[reply]

Will you ever stop pushing your distinctive style of presenting lattices graphically? Just write a standard work on lattice theory and get it published, and with some luck sooner or later people will start using your conventions. We can wait. Hans Adler 17:46, 15 March 2010 (UTC)[reply]

Seems, you rather judge me than the diagram. Could you simply tell us, why the left diagram should be better, or more standard than the right one?

I will be happy to hear about the convention how to draw Hasse diagrams, followed by the left, and broken by the right one. You may add it to the article Hasse diagram, so that stupid people like me won't produce crop like the right diagram again. Thanks. Lipedia (talk) 18:39, 15 March 2010 (UTC)[reply]

The older diagram (the one on the left) is clearly better:

It doesn't need a separate key
It more clearly respects the rank structure of this ranked lattice
It makes the number of elements per rank more obvious — in the one on the right, the upper middle rank is shown as narrower than the lower middle rank even though it has more elements
It is a little more compact overall

In exchange, it doesn't show some of the symmetrical substructures that the other one does, but are these substructures important? If one diagram showed symmetries of the whole lattice that the other didn't, that would be one thing, but why are these particular substructures worth showing? —David Eppstein (talk) 21:17, 15 March 2010 (UTC)[reply]

Well. That's how an answer look's.

Since I included the descriptions, the right file doesn't need a seperate key anymore.

(The lexicographical ennumeration of the knots could still be removed.)

If the main authors of the article concider the rank structure that important, this may be a reason to keep the old file. Although I think it's quite visible, that the right one has a "second floor", inhabited by seven knots. I arranged 8,9,10 vertically, to avoid crossed lines.

I think the value of the right graph is primarily, that it is easier kept in mind, and thus (as I think) easier understood. But one may differ about this point, and in the end, the main authors get what they want. Greetings, Lipedia (talk) 22:01, 15 March 2010 (UTC)[reply]

Merger proposal

Someone has proposed to merge this article with partially ordered set. While I am a great merger myself, I strongly disagree in this case. Lattices are not just a special case of partial orders in which any two elements have a least upper bound and a greatest lower bound. Even though the objects are the same in the finite case, we have the following crucial differences that are hard to handle in a single article:

Infinite partial orders are normally not lattices at all.
Even in the finite case, a homomorphism between partial orders (order-preserving map) is not normally a lattice homomorphism (sup- and inf-preserving map).
Partial orders can (in general) only be understood as relational structures. Lattices, on the other hand, also have an alternative interpretation as algebraic structures.

General order theory on one hand and lattice theory on the other hand are very different subjects. While each comes up at the beginning of a course that teaches the other, it makes no sense to cram them into a single article. Both articles are already big enough to stand on their own, each with potential for more, and there would be no synergy effects from merging, only confusion. Hans Adler 15:42, 25 April 2010 (UTC)[reply]

I am in complete agreement with you. I'm going to be WP:BOLD and remove the merge tags. —David Eppstein (talk) 16:12, 25 April 2010 (UTC)[reply]

Indeed. Paul August ☎ 16:42, 25 April 2010 (UTC)[reply]

Definition seems to contain a redundancy

"... in which any two elements have a unique supremum (the elements' least upper bound; called their join) and an infimum (greatest lower bound; called their meet)..."

I am under the impression that any two elements of a poset either do or don't have a supremum (join). If they do have a supremum, then the supremum is provably unique. It is therefore tautologous to say that any two elements are required to have a "unique" supremum. The current definition seems to acknowledge this by omitting the requirement that the infimum must be unique (although the wording is indeed slightly ambivalent in this regard).

Bottom line: I suggest dropping the word "unique". Am I missing something? CarlosChio (talk) 12:00, 22 November 2010 (UTC)[reply]

In the poset in which a,b are both above c,d, then a and b are both minimal upper bounds of c and d, but there is not one unique minimal upper bound. The "unique" is to emphasize that this sort of situation isn't good enough. —David Eppstein (talk) 16:46, 22 November 2010 (UTC)[reply]

Economics of persuasion?

The article says: "The algebraic interpretation of lattices plays an important role in universal algebra and in economics of persuasion." It is unclear what "economics of persuasion" refers to -- there should be a reference, or this should be deleted. Krifka (talk) 05:03, 2 August 2011 (UTC)[reply]

This was added without explanation by an anonymous editor on 4 April. It doesn't seem relevant to me, so I have simply removed it. Hans Adler 16:56, 2 August 2011 (UTC)[reply]

Join and meet of the empty set is not a convention

I edited the article that "defined" the join and meet of the empty set, and justified this "convention." It is neither a definition nor a convention, because it necessarily follows from the definition of join and meet, and the vacuous truth that every element must be a lower bound and upper bound of the empty set.

I thus removed the words "defined" and "convention," and, with hope, added sufficient text to explain how meet and join are derived. 149.125.250.184 (talk) 16:30, 27 April 2012 (UTC)[reply]

Explanation

This article suffers from the same problem that affects many mathematics articles. The article is written in the abstract, which is fine for many mathematicians who think very much in the abstract, but not sufficient for an encyclopaedia who's purpose is to make knowledge accessible to a wider audience. Specifically the article lacks an explanation of the purpose and relevance of Lattices in the real (non abstract) world and lacks examples of its application to problems that can be easily visualised by an audience with limited mathematical training. In my case, it is difficult for me to understand whether this branch of mathematics would be useful to me or not. This is an important question as it determines whether I ought to invest time in learning it (or spend the time on something else).

Correcting the omission would help to bridge the gulf that exists between mathematicians and the rest of the population, to the benefit of both sides. FreeFlow99 (talk) 09:07, 25 August 2013 (UTC)[reply]

Applications: Suggest to distinguish between "must-be-lattice / is-usually-lattice" and "may-be-lattice"

Now that User:Nbarth has added Multiple inheritance to the section Lattice (order)#Applications that use lattice theory, I glanced at the list given there and found that some links refer to an application area that may use lattices, but need not. For example, a class structure based on multiple inheritance itself may be a lattice, or may be not (it could look e.g. like a non-lattice poset from Pic.6 or 7); as another example, an ontology (computer science) may be a lattice or not (again Pic.6 / 7); I didn't check the remaining entries. I think, these entries should be kept nevertheless, but should be collected after an own introductory text saying just the above. - Jochen Burghardt (talk) 19:36, 15 December 2013 (UTC)[reply]

Thank Jochen, this is a good point!

When updating this, I was thinking “actually, these are properly lattice-like structures – you don’t generally have joins or even always meets”. I agree that these are relevant to lattice theory, though they are not generally lattices, but instead partial lattices. I’ve updated the page to include a (sourced) definition of partial lattice, and to include a note as suggested, as of this edit.

—Nils von Barth (nbarth) (talk) 15:19, 16 December 2013 (UTC)[reply]

Counter-examples

**Pic.7:** Non-lattice poset: b and c have common upper bounds d, e, and f, but no least one.

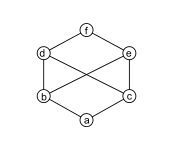
I'm not sure that Pic.7's description is correct. Why would f be a common upper bound for b and c, but a not be a common lower bound?

What defines a common bound? Can someone with better expertise on this subject verify this diagram and its description? — Dbechrd (talk) 17:25, 22 July 2014 (UTC)[reply]

I think you are misinterpreting the caption. a is a common lower bound. The reason this is not a lattice is different: it's because b and c have no lowest common upper bound. Among the three upper bounds d, e, and f, none is uniquely lowest. —David Eppstein (talk) 17:50, 22 July 2014 (UTC)[reply]

Sublattices

Every lattice has an empty sublattice - according to the general definition of substructure in universal algebra, or subobject in category theory. It is not natural to exclude it. -- Martin B. --92.228.253.9 (talk) 23:06, 2 August 2015 (UTC)[reply]

Need a dedicated page (or at least a longer subpage) on sublattices and also join-closed subsets and meet-closed subsets, as well as finitely join-closed subsets and finitely meet-closed subsets. --VictorPorton (talk) 15:21, 17 April 2016 (UTC)[reply]

Subsets of a lattice

I did not understand the following sentence:

It follows by an induction argument that every non-empty finite subset of a lattice has a join and a meet.

How can this be true? Consider poset on [4] with relations 1<2, 1<3, 2<4, 3<4, 1<4 (which is a lattice). The subset {2,3} does not have a join or a meet. — Preceding unsigned comment added by 62.46.197.84 (talk) 16:55, 19 November 2016 (UTC)[reply]

I think the sentence is ambiguous. When understood as "each non-empty finite subset of a lattice is again a lattice, having both a join and a meet operation", it is wrong, as your example shows. However, when understood as "each non-empty finite subset of a lattice has a greatest lower bound as well as a smallest upper bound", it is true, and in fact follows by induction on the set's cardinality. - Jochen Burghardt (talk) 18:27, 19 November 2016 (UTC)[reply]

Binary relation table

All I can see is green or red "✓":s - anyone who can explain what I should do ? Install support for Chinese ? Boeing720 (talk) 17:50, 11 October 2018 (UTC)[reply]

I see green checks and red X's, and the table looks completely normal. Is the problem that you're seeing all checkmarks? Otherwise I don't understand what you think is wrong. Rschwieb (talk) 18:45, 11 October 2018 (UTC)[reply]

In response to the above discussion, I added an explanation how to read the table. I hope it is understandable. - Jochen Burghardt (talk) 09:52, 12 October 2018 (UTC)[reply]

@Rschwieb: I did not intend to submit any complaint to this article. I just described how it looks to me, and simply wondered if anyone knew what might be wrong with my OS. Uncertain of how this -> ✓ <- sign looks to you, I describe it as like a framed square with "27" and "13" inside. Unicode ??? I have seen such signs before in other articles. But @Jochen Burghardt: I surmise the table is to be read like a binary pattern, and a question of "yes" =green or "no" =red. And whatever signs displayed, it's about the colours. Thanks for your efforts !

If anyone else have some kind of idea why I can't see "X"'es but these strange " ✓ -signs" instead, I wouldn't mind if that idea is shared with me. Again - this was not a complaint. Boeing720 (talk) 05:37, 13 October 2018 (UTC)[reply]

The fonts in your browser are messed up? Also the character you've copied and pasted is not an X, it's a check mark. Anyway, for more on why, see Unicode and HTML, and for more on how to fix it, see Help:Special characters. —David Eppstein (talk) 07:34, 13 October 2018 (UTC)[reply]

I thank you very much for this information. (the "X":es are meant to be displayed, according to user above, but I can't see them - I just copied what I can see) Never heard about check marks before. I will study your link. Thanks again ! Boeing720 (talk) 01:03, 14 October 2018 (UTC)[reply]

I guess you're correct on that it's somehow related to my browser (Firefox). Thank again Boeing720 (talk) 01:13, 14 October 2018 (UTC)[reply]

⊤ and ⊥, 0 and 1

The article mentions ⊤ and ⊥ but later in bounded lattices it says

"A bounded lattice is an algebraic structure of the form (L, ∨, ∧, 0, 1) such that (L, ∨, ∧) is a lattice, 0 (the lattice's bottom) is the identity element for the join operation ∨, and 1 (the lattice's top) is the identity element for the meet operation ∧."

I may be mistaken but there seems to be a mix of conventions in the same article, that ⊤ and 1 both used for top, ⊥ and 0 for bottom. I don't see that ⊤ is any more or less eligible to represent the uppermost element than 1, so is there redundant convention or something fundamental I'm missing?

Put another way, I think it's just saying 1 is a meta-variable denoting the uppermost element of L, exactly the same way ⊤ is elsewhere.

thanks 92.29.236.150 (talk) 21:46, 8 November 2018 (UTC)[reply]

I didn't find any occurrence of "⊤", "

\top

", "⊥", or "

\bot

" in the article, except in the one sentence where they are introduced as alternate notation for "0" and "1". (I added a similar sentence in response to your above issue, but then I noticed it was already explained before, therefore I undid my edit.) So I don't understand what is your problem. - Jochen Burghardt (talk) 11:55, 9 November 2018 (UTC)[reply]

I have only ever seen ⊤ and ⊥ used everywhere. The alternative notation of 1 and 0 is entirely new to me. Additionally the sentence "A bounded lattice is a lattice that additionally has a greatest element 1 and a least element 0, which satisfy..." suggested that 1 and 0 had some particular relevance to *bounded* lattices specifically.

Also the phrase "The greatest and least element is also called the maximum and minimum, or the top and bottom element, and denoted by ⊤ and ⊥". If I read it in the context of your reply I see they are obviously equivalent but that equivalence is not utterly explicit. If the first quoted sentence had said "...that additionally has a greatest element 1 (also called maximum, or top, or ⊤)..." there'd be no confusion for me. I'm not suggesting you change it, just explaining.

My confusion was over alternate terminology of 0 and 1, and the fact that I'm trying to learn lattices out of a couple of books (Vijay k. Garg's Introduction to Lattice Theory With Computer Science Applications, and Muchnick's Compiler Design & Implementation)with no-one to ask when that confusion strikes. It's incredibly easy to be misinterpret anything when you're a n00b. So, sorry to waste your time. FYI I'm trying to learn lattices to understand dataflow stuff in compilers. BTW this wiki article is bloody brilliant, it's been so helpful, so thank you everyone! 79.75.98.230 (talk) 12:59, 9 November 2018 (UTC)[reply]

I think 0 and 1 is often used in the theory of boolean algebras (which are particular kinds of lattices); in lattice theory ⊤ and ⊥ may be more common, as you said. Both ⊤,⊥ and their alternate notation 0,1 are relevant only for bounded lattices: when a top and a bottom element exists, the lattice is called bounded.

I've rephrased the sentence to make it more clear, and I'd like to read your opinion about the change.

I believe wikipedia should (eventually) be understandable to people like you who are learning some new stuff and see it for the first time. So it is not a waste of time to improve it to avoid misunderstandings. - Jochen Burghardt (talk) 18:30, 10 November 2018 (UTC)[reply]

To me that restatement seems about as unambiguous as english can possibly get, so an improvement in my eyes, and thank you. 92.29.229.95 (talk) 21:03, 11 November 2018 (UTC)[reply]

Mistake about bounded lattices in section 1?

imho the statement "A partially ordered set is a bounded lattice if and only if every finite set of elements (including the empty set) has a join and a meet." is wrong (see eg. Pic. 7 for a bounded poset). I guess a correct (and simpler) statement would be "A lattice is bounded if and only if the empty set of elements has a join and a meet.". Other (nonempty) finite sets are a matter of induction, and mentioned elsewhere. Am I right? — Preceding unsigned comment added by 187.3.207.124 (talk) 11:49, 24 March 2019 (UTC)[reply]

Excuse me, I take it back. That sentence is correct. Somehow I read "a poset is bounded iff...", as if the existence of 0 and 1 granted meets and joins everywhere.187.3.207.124 (talk) 12:42, 24 March 2019 (UTC)[reply]

Counter example ?

"This definition makes ∨ and ∧ binary operations. Both operations are monotone with respect to the order: a1 ≤ a2 and b1 ≤ b2 implies that a1 ∨ b1 ≤ a2 ∨ b2 and a1 ∧ b1 ≤ a2 ∧ b2."

If we take a1 = 5, b1 = 5, a2 = 6 and b2 = 8 and use the LGM, GCD as the binary operations, then the assertion above doesn't appear to hold. a1 <= a2 and b1 <= b2, but a1 ^ b1 is 5 while a2 ^ b2 is 2, so a1 ∧ b1 ≤ a2 ∧ b2 doesn't hold.

— Preceding unsigned comment added by Sophianto (talk • contribs) 06:48, 15 May 2020 (UTC)[reply]

With these operations, it is not true that a1 ≤ a2 nor that b1 ≤ b2, because (for these operations), the comparison operation is by divisibility, not numerical value. —David Eppstein (talk) 07:28, 15 May 2020 (UTC)[reply]

Join and meet on finite sets

The article states that "one can think of join and meet as binary operations that are defined on non-empty finite sets, rather than on elements". I interpret this as operations $\bigvee$ and $\bigwedge$ on sets as defined earlier in the article, e.g. $a\vee b\vee c$ is rewritten to $\bigvee \{a,b,c\}$ , but then the operations $\bigvee$ and $\bigwedge$ are not binary. Is my understanding incorrect, or is the word binary incorrect? — Preceding unsigned comment added by 131.174.142.107 (talk • contribs)

I think you're right. If you remove "binary" I would also change it to "rather than on pairs of elements". —David Eppstein (talk) 17:51, 23 July 2019 (UTC)[reply]

Distributivity (section 8.3)

I'm confused what the article is claiming (and that's not clarified in the linked article on Distributive Lattice).

The narrative to Pic 11 says that the N5 lattice violates one distributivity equation, but satisfies its dual.

The main body gives those equations (but with different variable names and in reverse order) then says

> A lattice that satisfies the first or, equivalently (as it turns out), the second axiom, ...

If N5 satisfies the second but not the first, those equations can't be equivalent?

Does it mean the first equation implies the second, but not v.v.? AntC2 (talk) 23:37, 4 October 2019 (UTC)[reply]

Ah, I think I can see what's going on. But it's not well explained.

The laws given in the main body must hold for all elements a, b, c. Whereas the narrative to Pic 11 is talking about specific nodes labelled a, b, c. Some suggestions:

Use distinct variable names for the nodes in Pic 11, maybe d, e, f instead of a, b, c.

Note that the laws are to hold for all choices of three elements, suggested wording

> A lattice that satisfies the first law for all elements a, b, c or, equivalently (as it turns out), the second axiom, ...

Expand the narrative to Pic 11 to show both laws are violated by specific assignments of nodes, suggested wording

> The labelled elements violate the distributivity equations c ∧ (a ∨ b) = (c ∧ a) ∨ (c ∧ b) and b ∨ (a ∧ c) = (b ∨ a) ∧ (b ∨ c), > but satisfy their duals c ∨ (a ∧ b) = (c ∨ a) ∧ (c ∨ b) and b ∧ (a ∨ c) = (b ∧ a) ∨ (b ∧ c). — Preceding unsigned comment added by AntC2 (talk • contribs) 01:48, 5 October 2019 (UTC)[reply]

Should link to article "Greatest element and least element"

which is at Top element (which oddly calls itself "Greatest element and least element" which it claims was "(Redirected from Top element)" but the URL is as given above, ending in /Top_element - wut??).

Any reason not to, because it would have been a good to have known about this WRT my earlier question here Talk:Lattice (order) § ⊤ and ⊥, 0 and 1. If there is already such a link I can't find it. 79.75.122.175 (talk) 20:32, 7 August 2021 (UTC)[reply]

You may want to read Wikipedia:Redirect, that should clarify a thing or two for you. As regards the link you want added, please note that both greatest element and least element already redirect to greatest element and least element. Paradoctor (talk) 20:55, 7 August 2021 (UTC)[reply]

Will check the redirect info, thanks. Didn't find the links you gave because I was looking for the whole title rather than just parts ie. didn't look just for 'greatest element'. Much obliged. 79.75.122.175 (talk) 21:16, 7 August 2021 (UTC)[reply]

Non-distributive lattices

I think @Timeroot is right in that the current article gives WP:UNDUE weight to distributive lattices. The examples in the lead are distributive, and pretty much all the other examples are too; the only non-distributive examples are (confusingly enough) found in the distributive lattices section. In actual mathematics distributive lattices are common but so are non-distributive lattices; the article should not be solely about one or the other, and particularly considering that Distributive lattice is a page, I would say this article should lean towards discussing non-distributive examples. Mathnerd314159 (talk) 21:20, 28 January 2024 (UTC)[reply]

Hi, thanks. @Jochen Burghardt, is the only objection that it messed up the numbering of the pictures? I can fix that. Or is there some other objection to the choice of pictures (too many, too 'busy' as pictures?). Let me know. Timeroot (talk) 16:55, 29 January 2024 (UTC)[reply]

Having messed up the numbers (and having duplicated the N5 and M3 picture) is my only strong objection. For your A4*C2 image, I'd prefer a less complex version, e.g. similar to File:Octahedral subgroup tree tidy.svg, where in interior details of vertices are omitted, but I wouldn't insist on that. While I understand Pic.1-5, I understand none of your new non-distributive examples, but this may be a matter of my (missing) foreknowledge. Nevertheless, if it was possible to add some easier examples, I'd appreciate that, and I guess, many readers would, too. - Jochen Burghardt (talk) 19:00, 29 January 2024 (UTC)[reply]